pp品牌全称是什么！

相位这个概念，在量子力学中如同位置和动量在经典力学中一样，都是基础性的。虽然量子波函数的相位常被视为不可观测的数学产物，但迈克尔·贝里于1984年发表的划时代论文《伴随绝热变化的量子相位因子》（"Quantal phase factors accompanying adiabatic changes"）不可逆转地确立了其物理实在性及深远影响。这项工作向世界介绍了如今广为人知的贝里相位，或称几何相位，揭示了量子演化中一种先前隐藏的拓扑特征，此后渗透到物理学的几乎每个子领域乃至更广阔的范畴。

在贝里取得突破之前，量子力学中对绝热演化的普遍理解主要由绝热定理概括。该定理指出，如果一个量子系统的哈密顿量变化得足够缓慢，系统将保持在其瞬时本征态上。在此类演化中获得的相位曾被认为仅仅是“动力学”的，是能量对时间积分的结果，与演化持续时间和态的能量直接成比例。贝里的过人之处在于他认识到这种图景是不完整的。他证明，除了这种熟悉的动力学相之外，还会积累一个额外的、路径依赖的“几何”相位，这个相位完全独立于演化速率，并且只取决于哈密顿量参数空间中系统参数所描绘的闭合回路。

贝里相位的本质在于其几何起源。想象一个量子系统，其哈密顿量在参数空间中沿着一个闭合回路平滑地变化。例如，一个自旋在磁场中缓慢旋转方向，然后回到其初始方向。根据绝热定理，自旋将保持与瞬时磁场对齐。然而，贝里表明，在回到初始态时，波函数会获得一个额外的相位因子。这个相位不取决于回路遍历的速度，而仅仅取决于回路本身的形状，类似于回路在参数空间中某个奇点处所张的立体角。这种与演化速率的深刻独立性正是几何相与动力学相的区别所在，并且使其成为在不跨越简并点的情况下，路径连续变形下的一个拓扑不变量。

对于在参数空间 R 中沿着闭合路径 C 绝热演化的本征态 ∣n(R)⟩ 的贝里相 γn(C)，其数学表达式为：

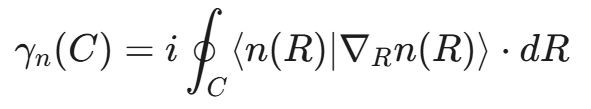
这个积分，当考虑其微分形式时常被称为贝里联络或贝里曲率，完美地捕捉了相位的几何性质。表达式 ⟨n(R)∣∇Rn(R)⟩ 代表了参数空间中的一个联络一形式，其在闭合回路上的积分是一个拓扑量。这种表述不仅提供了一个稳健的理论框架，还提供了一种计算这种先前未被注意到的相位的方法。

贝里发现的意义是即时且深远的。他认识到，物理学中一些看似不相关的现象，都可以被优雅地解释为这种新识别的几何相位的表现。一个典型的例子是阿哈罗诺夫-玻姆效应（AB effect），其中带电粒子即使被限制在磁场为零的区域，也会受到磁场的影响。AB 效应先前是用电磁矢量势来理解的，但贝里将其重新解释为几何相位的一个具体实例，其中电子在无场区域的路径所包围的磁通量充当了决定相移的几何量。同样，自旋在旋转时的符号反转，即一个自旋1/2粒子旋转360度后回到原始态时带有负号，也被证明是贝里相位的一种体现。这些例子强调了他的发现的普适性和基础性。

《伴随绝热变化的量子相位因子》的影响波及整个凝聚态物理领域，催生了拓扑物态这一新兴领域。贝里相位，以及其推广至贝里曲率和陈数的概念，成为表征和分类具有奇异电子性质的新型材料不可或缺的工具。例如，拓扑绝缘体是体态绝缘但其边缘或表面导电的材料，这一特性与电子在材料动量空间中遍历时累积的非平庸贝里相位直接相关。这个概念在理解量子霍尔效应、外尔半金属和狄拉克半金属以及各种其他拓扑态方面也起着关键作用。

除了凝聚态物理，贝里相还在物理学的各个领域找到了应用。在原子和分子物理学中，它对于理解分子动力学至关重要，特别是在涉及势能面锥形交叉的情况下，其中电子态变得简并。在量子光学中，它有助于解释光通过扭曲光纤时偏振的旋转。在量子信息科学中，几何相位为稳健的量子计算提供了一条潜在途径，因为几何门相较于传统的动力学门，对某些类型的环境噪声具有固有的更低敏感性。甚至在宇宙学和高能物理学中，几何相位的类似概念也在规范理论和引力场背景下得到了探索。

贝里1984年论文的持久遗产不仅在于其精确的数学公式或其直接的解释力，更在于其概念上的转变。它迫使物理学家重新思考看似简单的绝热演化过程，并认识到几何与量子力学之间深刻的相互作用。它证明，即使系统看似回到了初始状态，它所遍历的路径的“记忆”也可以被编码在其相位中，这种记忆本质上是拓扑的，并且独立于所花费的时间。这一发现开辟了全新的研究途径，将拓扑和几何的抽象数学概念与具体的物理现象联系起来。